姜晨瑞的博客

记录与总结

数据结构和算法学习

发表于 更新于 分类于 阅读次数： Valine：
本文字数： 56k 阅读时长 ≈ 51 分钟
数据结构是计算机内部数据的组织形式和存储方法，常用的数据结构有线性结构、数结构、图结构;本文对常用的查找和排序算法进行了总结并实现

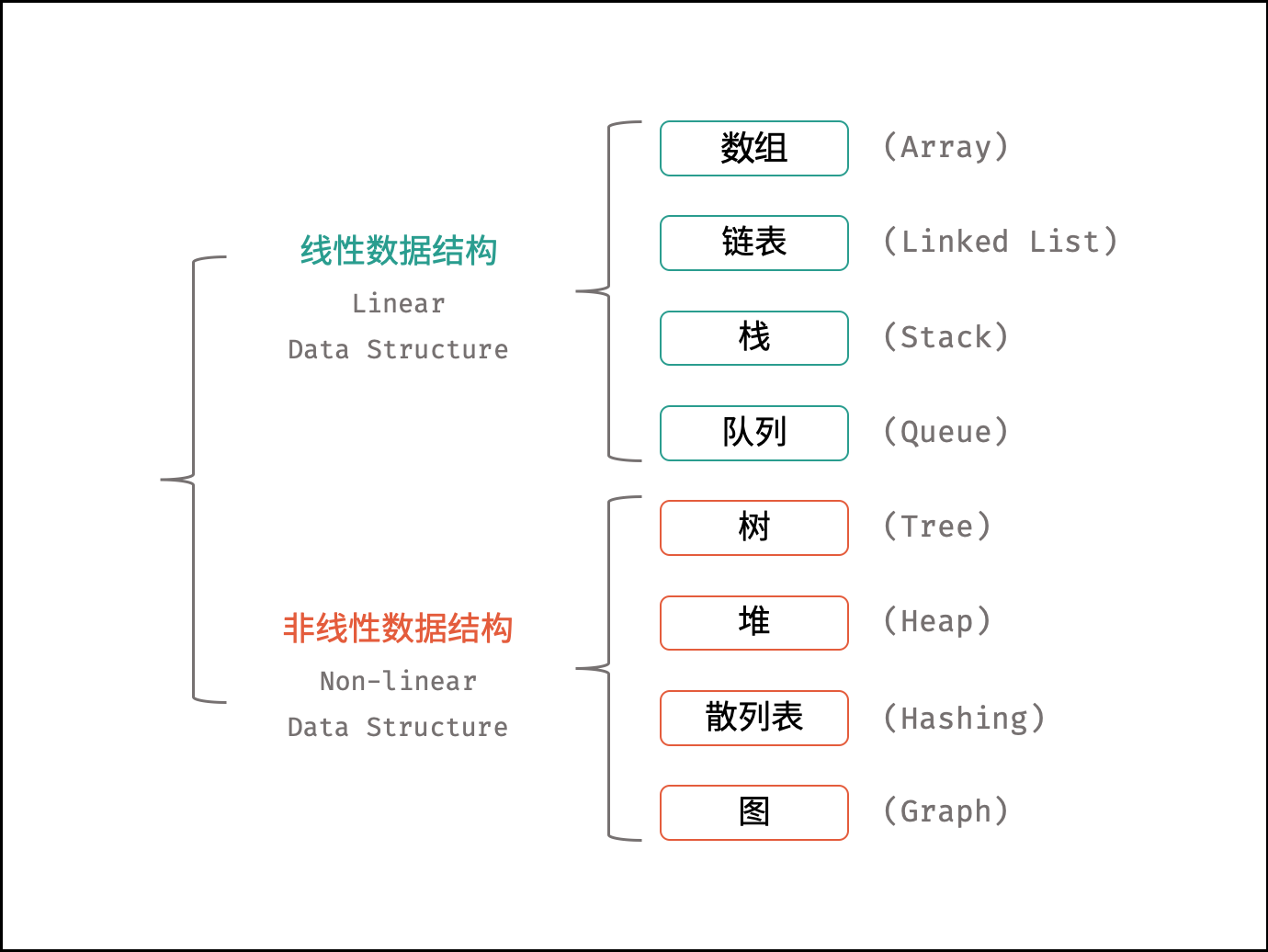
数据结构

数据结构是计算机内部数据的组织形式和存储方法，常用的数据结构有线性结构、数结构、图结构。

数据结构

线性结构

线性结构主要包括：顺序表、链表、栈、队列等基本形式。其中顺序表和链表是从存储形式上（或物理结构上）区分的，而栈和队列是从逻辑功能上区分的。也就是说，顺序表和链表是线性数据结构的基础，队列和栈是基于顺序表和链表的，它们由顺序表或链表构成。

栈的实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
#ifndef STACK_HPP
#define STACK_HPP
#include <iostream>
using namespace std;

template <class T>
class Stack {
public:
    Stack();
    Stack(int capacity);
    ~Stack();
    bool IsEmpty();                 // 判断是否为空
    bool IsFull();                  // 判断栈是否已满
    void ClearStack();              // 清空栈
    int Length();                   // 获取栈的长度
    bool Push(const T &element);    // 获取元素
    bool Pop(T &ele);               // 弹出栈顶元素
    void StackTraverse();           // 遍历栈

private:
    T *m_stack;     // 容器
    int m_top;      // 栈顶
    int m_capacity; // 容器容量
};

template <typename T>
Stack<T>::Stack() {
    cout << "构造函数" << endl;
}

template <typename T>
Stack<T>::Stack(int capacity) {
    this->m_capacity = capacity;
    this->m_top = 0;
    this->m_stack = new T[this->m_capacity];
}

template <typename T>
Stack<T>::~Stack() {
    if (this->m_stack != NULL) {
        delete[] this->m_stack;
        this->m_stack = NULL;
    }
}

template <typename T>
bool Stack<T>::IsEmpty() {
    return this->m_top == 0 ? true : false;
}

template <typename T>
bool Stack<T>::IsFull() {
    return this->m_top == this->m_capacity ? true : false;
}

template <typename T>
void Stack<T>::ClearStack() {
    this->m_top = 0;
}

template <typename T>
int Stack<T>::Length() {
    return this->m_top;
}

template <typename T>
bool Stack<T>::Push(const T &element) {
    if (IsFull()) {
        return false;
    } else {
        this->m_stack[this->m_top++] = element;
        return true;
    }
}

template <typename T>
bool Stack<T>::Pop(T &ele) {
    if (!IsEmpty()) {
        this->m_top--;
        ele = this->m_stack[this->m_top];
        return true;
    } else {
        return false;
    }
}

template <typename T>
void Stack<T>::StackTraverse() {
    if (!IsEmpty()) {
        for (int i = m_top - 1; i >= 0; --i) {
            cout << this->m_stack[i] << ' ';
        }
        cout << endl;
    } else {
        cout << "栈为空" << endl;
    }
}
#endif

队列的实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
#ifndef MYQUEUE_HPP
#define MYQUEUE_HPP
#include <iostream>
using namespace std;

template <typename T>
struct QueueNode {
    T data;
    QueueNode *next;
    QueueNode () {
        this->next = NULL;
    }
};

template <class T>
class MyQueue {
public:
    MyQueue() {
        this->count = 0;
        this->head = new QueueNode <T>();
        this->tail = new QueueNode <T>();
        this->tail = this->head;
    }
    ~MyQueue() {
        if (this->head != NULL) {
            cout << "释放head" << endl;
            delete[] this->head;
            this->head = NULL;
        }
        if (this->tail != NULL) {
            cout << "释放tail" << endl;
            delete[] this->tail;
            this->tail = NULL;
        }
    }
    int size() {
        return this->count;
    }
    bool IsEmpty() {
        if (size() == 0) {
            return true;
        } else {
            return false;
        }
    }
    void InQueue(T val) {
        QueueNode <T> *temp = new QueueNode<T>();
        temp->data = val;
        this->tail->next = temp;
        this->tail = temp;
        this->count++;
    }
    QueueNode<T>* OutQueue() {
        if (this->count == 0) {
            cout << "队列为空" << endl;
            return NULL;
        }
        QueueNode <T> *temp = this->head->next;
        if (temp) {
            this->head->next = temp->next;
            temp->next = NULL;
            this->count--;
        }
        return temp;
    }
    void QueueTraverse() {
        if (this->count == 0) {
            cout << "队列为空" << endl;
            return;
        }
        QueueNode <T> *temp = head->next;
        while (temp) {
            cout << temp->data << ' ';
            temp = temp->next;
        }
        cout << endl;
    }
    void Remove() {
        this->head->next = NULL;
        this->tail = this->head;
        this->count = 0;
    }

private:
    int count;
    QueueNode <T> *head;
    QueueNode <T> *tail;
};

#endif

链表反转

使用两个节点pre和next，先用next保存当前节点的next指针，然后将当前节点next指针指向上一个节点pre，接下来将当前节点赋值给pre，next赋值给当前节点进行下一循环，直到当前节点为NULL。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
struct ListNode {
	int val;
	struct ListNode *next;
	ListNode(int x) : val(x), next(NULL) {}
};

/**
 * 链表反转
 */
ListNode* ReverseList(ListNode *pHead) {
    if(pHead == NULL)
        return NULL;
    ListNode *pre = NULL;
    ListNode *next = NULL;
    while (pHead != NULL) {
        next = pHead->next;
        pHead->next = pre;
        pre = pHead;
        pHead = next;
    }
    return pre;
}

寻找第k大

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
int Partition(vector<int> &arr, int start, int end) {
    // 降序排列
    if (start == end)
        return start;
    int left = start, right = end, key = arr[start];
    while (left < right) {
        while (left < right && arr[right] <= key)
            right--;
        arr[left] = arr[right];
        while (left < right && arr[left] >= key)
            left++;
        arr[right] = arr[left];
    }
    arr[left] = key;
    return left;
}

/**
 * 寻找第k大
 */
int findKth(vector<int> a, int n, int K) {
    int low = 0;
    int high = n - 1;
    int mid;
    while (low <= high) {
        mid = Partition(a, low, high);
        if (K < mid + 1) {
            // 在左半段
            high = mid - 1;
        } else  if (K > mid + 1) {
            // 在右半段
            low = mid + 1;
        } else {
            return a[mid];
        }
    }
    return -1;
}

括号序列

给出一个仅包含字符’(‘,’)’,’{‘,’}’,’[‘和’]’,的字符串，判断给出的字符串是否是合法的括号序列，括号必须以正确的顺序关闭，”()”和”()[]{}”都是合法的括号序列，但”(]”和”([)]”不合法。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
bool isValid(string s) {
    // 如果字符串长度不是偶数，则不合法
    if (s.size() & 1 != 0)
        return false;
    stack<char> temp;
    for (int i = 0; i < s.size(); ++i) {
        if (s[i] == '(' || s[i] == '{' || s[i] == '[')
            temp.push(s[i]);
        else {
            if (temp.empty())
                return false;
            switch (s[i]) {
                case '}':
                    if (temp.top() == '{')
                        temp.pop();
                    break;
                case ']':
                    if (temp.top() == '[')
                        temp.pop();
                    break;
                case ')':
                    if (temp.top() == '(')
                        temp.pop();
                    break;
                default:
                    return false;
            }
        }
    }
    if (!temp.empty())
        return false;
    return true;
}

链表中的节点每k有一组翻转

题目描述

将给出的链表中的节点每$k$个一组翻转，返回翻转后的链表
如果链表中的节点数不是$k$的倍数，将最后剩下的节点保持原样
你不能更改节点中的值，只能更改节点本身。
要求空间复杂度$O(1)$。
例如：
给定的链表是$1→2→3→4→5$

  • 对于 $k = 2$, 你应该返回 $2→1→4→3→5$
  • 对于 $k = 3$, 你应该返回 $3→2→1→4→5$
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
/**
 * 链表中的节点每k有一组翻转
 * @param head
 * @param k
 * @return
 */
ListNode* reverseKGroup(ListNode* head, int k) {
    if (head == NULL)
        return NULL;
    ListNode *temp = head;
    int len = 0;
    while (temp != NULL) {
        temp = temp->next;
        ++len;
    }
    temp = head;
    if (len < k)
        return head;
    ListNode *pre = NULL;
    ListNode *next = NULL;
    for (int i = 0; i < k; ++i) {
        next = head->next;
        head->next = pre;
        pre = head;
        head = next;
    }
    temp->next = reverseKGroup(head, k);
    return pre;    
}

将字符串转换为整数

1
2
3
4
5
6
7
8
9
10
11
12
13
int StrToInt(string str) {
    if (str.empty())
        return 0;
    int res = 0;
    int mark = (str[0] == '-') ? -1 : 1;
    int i = (str[0] == '+' || str[0] == '-') ? 1 : 0;
    for (; i < str.size(); ++i) {
        if (str[i] < '0' || str[i] > '9')
            return 0;
        res = res*10 + str[i] - '0';
    }
    return res*mark;
}

数组中重复的数字

在一个长度为n的数组里的所有数字都在0到n-1的范围内。 数组中某些数字是重复的，但不知道有几个数字是重复的。也不知道每个数字重复几次。请找出数组中任意一个重复的数字。 例如，如果输入长度为7的数组{2,3,1,0,2,5,3}，那么对应的输出是第一个重复的数字2。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
bool duplicate(int numbers[], int length, int* duplication) {
    if (length == 0 || length == 1)
        return false;
    int *tempArr = new int[length]();
    for (int i = 0; i < length; ++i) {
        if (tempArr[numbers[i]] == 0)
            tempArr[numbers[i]] = 1;
        else {
            *duplication = numbers[i];
            return true;
        }
    }
    return false;
}

构建乘积数组

给定一个数组A[0,1,…,n-1],请构建一个数组B[0,1,…,n-1],其中B中的元素B[i]=A[0]A[1]…A[i-1]A[i+1]…A[n-1]。不能使用除法。（注意：规定B[0] = A[1] A[2] … A[n-1]，B[n-1] = A[0] A[1] … A[n-2];）
对于A长度为1的情况，B无意义，故而无法构建，因此该情况不会存在。

1
2
3
4
5
6
7
8
9
10
11
12
13
vector<int> multiply(const vector<int>& A) {
    vector<int> B(A.size(), 1);
    B[0] = 1;
    for (int i = 1; i < A.size(); ++i) {
        B[i] = B[i-1] * A[i-1];
    }
    int temp = 1;
    for (int j = A.size() - 1; j >= 0; j--) {
        B[j] *= temp;
        temp *= A[j];
    }
    return B;
}

表示数值的字符串

题目描述

请实现一个函数用来判断字符串是否表示数值（包括整数和小数）。例如，字符串”+100”,”5e2”,”-123”,”3.1416”和”-1E-16”都表示数值。 但是”12e”,”1a3.14”,”1.2.3”,”+-5”和”12e+4.3”都不是。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
bool isNumeric(char* str) {
    // 标记符号、小数点、e是否出现过
    bool sign = false, decimal = false, hasE = false;
    for (int i = 0; i < strlen(str); i++) {
        if (str[i] == 'e' || str[i] == 'E') {
            if (i == strlen(str)-1) return false; // e后面一定要接数字
            if (hasE) return false;  // 不能同时存在两个e
            hasE = true;
        } else if (str[i] == '+' || str[i] == '-') {
            // 第二次出现+-符号，则必须紧接在e之后
            if (sign && str[i-1] != 'e' && str[i-1] != 'E') return false;
            // 第一次出现+-符号，且不是在字符串开头，则也必须紧接在e之后
            if (!sign && i > 0 && str[i-1] != 'e' && str[i-1] != 'E') return false;
            sign = true;
        } else if (str[i] == '.') {
            // e后面不能接小数点，小数点不能出现两次
            if (hasE || decimal) return false;
            decimal = true;
        } else if (str[i] < '0' || str[i] > '9') // 不合法字符
            return false;
    }
    return true;
}

字符流中第一个不重复的字符

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
class Solution
{
public:
    Solution() {
        cnt = new int[128]();
    }
    ~Solution() {
        if (cnt != NULL)
            delete[] cnt;
        cnt = NULL;
    }
    void Insert(char ch) {
        ++cnt[ch - '\0'];
        if (cnt[ch - '\0'] == 1)
            data.push(ch);
    }
    char FirstAppearingOnce() {
        while (!data.empty() && cnt[data.front() - '\0'] > 1)
            data.pop();
        if (data.empty())
            return '#';
        return data.front();
    }

private:
    queue<char> data;
    int *cnt;
};

删除链表中重复的结点

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
// 删除链表中重复的结点
ListNode* deleteDuplication(ListNode* pHead) {
    ListNode *slow, *fast;
    ListNode *Head = new ListNode(0);
    Head->next = pHead;
    slow = Head;
    fast = Head->next;
    while (fast != NULL) {
        if (fast->next != NULL && fast->val == fast->next->val) {
            while (fast->next != NULL && fast->val == fast->next->val)
                fast = fast->next;
            slow->next = fast->next;
            fast = fast->next;
        } else {
            slow = slow->next;
            fast = fast->next;
        }
    } 
    return Head->next;
}

两两交换链表中的节点

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
ListNode* swapPairs(ListNode* head) {
    ListNode* res = new ListNode(0);
    res->next = head;
    ListNode* first = res;
    while (first->next != NULL && first->next->next != NULL) {
        ListNode* second = first->next;
        ListNode* third = first->next->next;

        first->next = third;
        second->next = third->next;
        third->next = second;

        first = second;
    }
    return res->next;
}

字符串的排列

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
// 后剪枝
void dfs(string s, int start, set<string>& res) {
    if (s.size() == start) {
        res.insert(s);
        return;
    }
    for (int i = start; i < s.size(); ++i) {
        swap(s[i], s[start]);
        dfs(s, start+1, res);
        swap(s[i], s[start]);
    }
}
// 过程中剪枝
void dfs(string s, int start, vector<string>& res) {
    if (s.size() == start) {
        res.push_back(s);
        return;
    }
    set<char> st;
    for (int i = start; i < s.size(); ++i) {
        if (st.count(s[i])) continue;
        st.insert(s[i]);
        swap(s[i], s[start]);
        dfs(s, start+1, res);
        swap(s[i], s[start]);
    }
}
vector<string> permutation(string s) {
    vector<string> res;
    dfs(s, 0, res);
    return res;
}

滑动窗口的最大值

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
// 滑动窗口的最大值
int findMax(const vector<int> nums, int i, int j) {
    int maxval = nums[i];
    for (; i <= j; ++i) {
        maxval = max(maxval, nums[i]);
    }
    return maxval;
}
vector<int> maxSlidingWindow(vector<int>& nums, int k) {
    vector<int> ans;
    if (nums.size() == 0)
        return ans;
    int maxval = findMax(nums, 0, k-1);
    ans.push_back(maxval);
    for (int j = k, i = 1; j < nums.size(); ++j, ++i) {
        if (nums[j] > maxval)
            maxval = nums[j];
        else if (nums[i-1] == maxval)
            maxval = findMax(nums, i, j);
        ans.push_back(maxval);
    }
    return ans;
}

字符串转换为整数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
int strToInt(string str) {
    int res = 0, bndry = INT_MAX / 10;
    int i = 0, sign = 1, length = str.size();
    if (length == 0)
        return 0;
    while (str[i] == ' ')
        if (++i == length) return 0;
    if (str[i] == '-') sign = -1;
    if (str[i] == '-' || str[i] == '+') i++;
    for (int j = i; j < length; j++) {
        if (str[j] < '0' || str[j] > '9') break;
        if (res > bndry || res == bndry && str[j] > '7')
            return sign == 1 ? INT_MAX : INT_MIN;
        res = res * 10 + (str[j] - '0');
    }
    return sign*res;
}

双指针

调整数组顺序是奇数位于偶数前面

1
2
3
4
5
6
7
8
9
vector<int> exchange(vector<int> &nums) {
    int start = 0, end = nums.size() - 1;
    while (start < end) {
        while (nums[start] % 2 != 0) start++;
        while (nums[end] %2 == 0) end--;
        swap(nums[start], nums[end]);
    }
    return nums;
}

和为s的两个数字

1
2
3
4
5
6
7
8
9
10
11
12
13
vector<int> twoSum(vector<int>& nums, int target) {
    int start = 0, end = nums.size() - 1;
    vector<int> res;
    while (start < end) {
        if (nums[start] + nums[end] == target) {
            res.push_back(nums[start]);
            res.push_back(nums[end]);
            return res;
        } else if (nums[start] + nums[end] < target) start++;
        else end--;
    }
    return res;
}

判断链表中是否有环

链表和快慢指针

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
/**
 * 判断给定的链表是否有环
 * @param head
 * @return
 */
bool hasCycle(ListNode *head) {
    ListNode *low, *quick;
    low = quick = head;
    while (quick->next->next != NULL && quick->next != NULL) {
        low = low->next;
        quick = quick->next->next;
        if (low == quick)
            return true;
    }
    return false;
}

链表中环的入口

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
ListNode *detectCycle(ListNode *head) {
    if (head == NULL)
        return 0;
    ListNode *slow = head;
    ListNode *fast = head;
    while (fast != NULL && fast->next != NULL) {
        slow = slow->next;
        fast = fast->next->next;
        if (slow == fast)
            break;
    }
    if (fast == NULL || fast->next == NULL)
        return NULL;
    fast = head;
    while (slow != fast) {
        slow = slow->next;
        fast = fast->next;
    }
    return slow;
}

合并有序链表

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
ListNode* mergeTwoLists(ListNode* l1, ListNode* l2) {
    ListNode *head = new ListNode(-1);
    ListNode *temp = head;
    while (l1 != NULL || l2 != NULL) {
        if (l1 == NULL) {
            temp->next = l2;
            break;
        }
        if (l2 == NULL) {
            temp->next = l1;
            break;
        }
        if (l1->val < l2->val) {
            temp->next = l1;
            l1 = l1->next;
        } else {
            temp->next = l2;
            l2 = l2->next;
        }
        temp = temp->next;
    }
    return head->next;
}

删除链表的倒数第N个节点

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
/**
 * 删除链表倒数第N个节点
 * @param head ListNode类 
 * @param n int整型 
 * @return ListNode类
 */
ListNode* removeNthFromEnd(ListNode* head, int n) {
    if (head == NULL)
        return NULL;
    ListNode *dummy = new ListNode(0);
    dummy->next = head;
    head = dummy;
    ListNode *slow = head;
    ListNode *fast = head;
    for (int i = 0; i < n; ++i) {
        fast = fast->next;
    }
    while (fast->next != NULL) {
        slow = slow->next;
        fast = fast->next;
    }
    ListNode *temp = slow->next;
    slow->next = slow->next->next;
    delete temp;
    return dummy->next;
}

两个链表相加生成相加链表

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
/**
 * 两个链表相加生成相加链表
 */
ListNode* addInList(ListNode* head1, ListNode* head2) {
    stack<ListNode *> s1;
    stack<ListNode *> s2;
    while (head1) {
        s1.push(head1);
        head1 = head1->next;
    }
    while (head2) {
        s2.push(head2);
        head2 = head2->next;
    }
    int flag = 0;
    while (!s1.empty() || !s2.empty()) {
        int sum = flag;
        if (!s1.empty()) {
            sum += s1.top()->val;
            head1 = s1.top();
            s1.pop();
        }
        if (!s2.empty()) {
            sum += s2.top()->val;
            if (s2.size() > s1.size())
                head1 = s2.top();
            s2.pop();
        }
        if (sum < 10) {
            head1->val = sum;
            flag = 0;
        } else {
            head1->val = sum % 10;
            flag = sum / 10;
        }
    }
    if (flag > 0) {
        ListNode *head = new ListNode(flag);
        head->next = head1;
        return head;
    }
    return head1;
}

翻转单词顺序

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
vector<string> split(const string &str, const string &splitChar) {
    vector<string> res;
    if (str == "")
        return res;
    string strs = str + splitChar;
    size_t pos = strs.find(splitChar);

    while (pos != strs.npos) {
        string temp = strs.substr(0, pos);
        if (temp != " " && temp != "")
            res.push_back(temp);
        strs = strs.substr(pos+1, strs.size());
        pos = strs.find(splitChar);
    }
    return res;
}
string reverseWords(string s) {
    string res;
    const string splitChar = " ";
    vector<string> store = split(s, splitChar);
    if (store.size() == 0)
        return "";
    int len = store.size() - 1;
    res = store[len--];
    while(len >=0) {
        res += " " + store[len--];
    }
    return res;
}

多数之和问题

  • 三数之和
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
class ThreeSum {
public:
    vector<vector<int>> threeSum(vector<int>& nums) {
        int n = nums.size();
        if (n < 3) return {};
        sort(nums.begin(), nums.end());
        vector<vector<int>> res;
        for (int i = 0; i < n - 2; ++i) {
            vector<vector<int>> temp = twoSum(nums, i+1, 0 - nums[i]);
            for (vector<int>& a : temp) {
                a.insert(a.begin(), nums[i]);
                res.push_back(a);
            }
            while (i < n - 2 && nums[i] == nums[i+1]) i++;
        }
        return res;
    }
private:
    vector<vector<int>> twoSum(vector<int>& nums, int start, int target) {
        int low = start, high = nums.size() - 1;
        vector<vector<int>> res;
        while (low < high) {
            int sum = nums[low] + nums[high];
            int left = nums[low], right = nums[high];
            if (sum < target) {
                while (low < high && nums[low] == left) low++;
            } else if (sum > target) {
                while (low < high && nums[high] == right) high--;
            } else {
                res.push_back({left, right});
                while (low < high && nums[low] == left) low++;
                while (low < high && nums[high] == right) high--;
            }
        }
        return res;
    }
};
  • 四数之和
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
class Solution {
public:
    vector<vector<int>> fourSum(vector<int>& nums, int target) {
        sort(nums.begin(), nums.end());
        return nSumTarget(nums, 4, 0, target);
    }
private:
    vector<vector<int>> nSumTarget(vector<int>& nums, int n, int start, int target) {
        int size = nums.size();
        vector<vector<int>> res;
        if (n < 2 || size < n) return res;
        if (n == 2) {
            int low = start, high = size - 1;
            while (low < high) {
                int left = nums[low], right = nums[high];
                int sum = left + right;
                if (sum < target) {
                    while (low < high && nums[low] == left) low++;
                } else if (sum > target) {
                    while (low < high && nums[high] == right) high--;
                } else {
                    res.push_back({left, right});
                    while (low < high && nums[low] == left) low++;
                    while (low < high && nums[high] == right) high--;
                }
            }
        } else {
            for (int i = start; i < size; ++i) {
                vector<vector<int>> sub = nSumTarget(nums, n-1, i+1, target-nums[i]);
                for (vector<int>& arr : sub) {
                    arr.insert(arr.begin(), nums[i]);
                    res.push_back(arr);
                }
                while (i < size-1 && nums[i] == nums[i+1]) i++;
            }
        }
        return res;
    }
};

树结构

数据之间存在“一对多”的关系构成了树结构。

二叉树中序遍历

递归方法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
void inorder(TreeNode *node, vector<int> &res) {
    if (node == NULL)
        return;
    inorder(node->left, res);
    res.push_back(node->val);
    inorder(node->right, res);
}

// 二叉树中序遍历
vector<int> inorderTraversal(TreeNode* root) {
    vector<int> res;
    inorder(root, res);
    return res;
}

非递归方法

1
2
3
4
5
6
7
8
9
10
11
12
13
vector<int> inorderTraversal(TreeNode* root) {
    vector<int> res;
    stack<TreeNode*> node;
    while (root != NULL || !node.empty()) {
        for (; root != NULL; root = root->left) {
            node.push(root);
        }
        res.push_back(node.top()->val);
        root = node.top()->right;
        node.pop();
    }
    return res;
}

验证二叉搜索树

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
// 验证二叉搜索树
bool isValidBST(TreeNode* root) {
    stack<TreeNode*> stack;
    long long inorder = INT32_MIN - 1;
    while (root != NULL || !stack.empty()) {
        for (; root != NULL; root = root->left)
            stack.push(root);
        if (stack.top()->val <= inorder)
            return false;
        inorder = stack.top()->val;
        root = stack.top()->right;
        stack.pop();
    }
    return true;
}

二叉树的第k大节点

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
int kthLargest(TreeNode* root, int k) {
    if (root == NULL)
        return 0;
    stack<TreeNode*> node;
    int num = 1;
    while (root != NULL || !node.empty()) {
        for (; root != NULL; root = root->right) {
            node.push(root);
        }
        root = node.top()->left;
        if (num == k)
            return node.top()->val;
        node.pop();
        num++;
    }
    return 0;
}

二叉树前序遍历

递归方法

1
2
3
4
5
6
7
8
9
10
11
12
13
void preorder(TreeNode* node, vector<int> &res) {
    if (!node)
        return;
    res.push_back(node->val);
    preorder(node->left, res);
    preorder(node->right, res);
}
// 二叉树前序遍历
vector<int> preorderTraversal(TreeNode* root) {
    vector<int> res;
    preorder(root, res);
    return res;
}

非递归方法

1
2
3
4
5
6
7
8
9
10
11
12
13
vector<int> preorderTraversal(TreeNode* root) {
    vector<int> res;
    stack<TreeNode*> node;
    while (root!=NULL || !node.empty()) {
        for (; root!=NULL; root = root->left) {
            res.push_back(root->val);
            node.push(root);
        }
        root = node.top()->right;
        node.pop();
    }
    return res;
}

二叉树后序遍历

递归方法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
void postorder(TreeNode* node, vector<int> &res) {
    if (!node)
        return;
    postorder(node->left, res);
    postorder(node->right, res);
    res.push_back(node->val);
}

// 二叉树后序遍历
vector<int> postorderTraversal(TreeNode* root) {
    vector<int> res;
    postorder(root, res);
    return res;
}

非递归方法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
vector<int> postorderTraversal(TreeNode* root) {
    vector<int> res;
    stack<TreeNode*> node;
    TreeNode *cur = root;
    while (cur != NULL || !node.empty()) {
        while (cur) {
            res.push_back(cur->val);
            node.push(cur);
            cur = cur->right;
        }
        cur = node.top()->left;
        node.pop();
    }
    reverse(res.begin(), res.end());
    return res;
}

二叉树层序遍历

递归方法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
void levelOrder(TreeNode* root, int level, vector<vector<int>> &v) {
    if (root == NULL)
        return;
    if (v.size() < level + 1)
        v.resize(level + 1);
    v[level].push_back(root->val);
    levelOrder(root->left, level+1, v);
    levelOrder(root->right, level+1, v);
}
// 二叉树的层序遍历
vector<vector <int>> levelOrder(TreeNode* root) {
    vector<vector <int>> res;
    levelOrder(root, 0, res);
    return res;
}

非递归

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
vector<vector <int>> levelOrder(TreeNode* root) {
    vector<vector <int>> res;
    if (root == NULL)
        return res;
    queue<TreeNode*> q;
    q.push(root);
    int level = 0;
    while (!q.empty()) {
        int size = q.size();
        res.push_back(vector<int>());
        for (int i = 0; i < size; ++i) {
            TreeNode* temp = q.front();
            q.pop();
            res[level].push_back(temp->val);
            if (temp->left != NULL)
                q.push(temp->left);
            if (temp->right != NULL)
                q.push(temp->right);
        }
        ++level;
    }
    return res;
}

二叉树的锯齿形层次遍历

递归

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
void zigzagLevel(TreeNode* node, int level, vector<vector <int>> &res) {
    if (node == NULL)
        return;
    if (res.size() < level + 1)
        res.push_back(vector<int>());
    if (level % 2 == 0)
        res[level].push_back(node->val);
    else
        res[level].insert(res[level].begin(), node->val);
    zigzagLevel(node->left, level+1, res);
    zigzagLevel(node->right, level+1, res);    
}
// 二叉树的锯齿形层次遍历
vector<vector <int>> zigzagLevelOrder(TreeNode* root) {
    vector<vector <int>> res;
    zigzagLevel(root, 0, res);
    return res;
}

非递归
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
vector<vector <int>> zigzagLevelOrder(TreeNode* root) {
    vector<vector <int>> res;
    if (root == NULL)
        return res;
    queue<TreeNode*> q;
    int level = 0;
    q.push(root);
    while (!q.empty()) {
        int size = q.size();
        res.push_back(vector<int>());
        for (int i = 0; i < size; ++i) {
            TreeNode* temp = q.front();
            q.pop();
            if (level % 2 == 0)
                res[level].push_back(temp->val);
            else
                res[level].insert(res[level].begin(), temp->val);
            if (temp->left != NULL)
                q.push(temp->left);
            if (temp->right != NULL)
                q.push(temp->right);
        }
        ++level;
    }
    return res;
}

二叉树的层次遍历2

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
vector<vector<int>> levelOrderBottom(TreeNode* root) {
    vector<vector <int>> res;
    if (root == NULL)
        return res;
    queue<TreeNode*> q;
    q.push(root);
    while (!q.empty()) {
        int size = q.size();
        vector<int> temp;
        for (int i = 0; i < size; ++i) {
            TreeNode* node = q.front();
            temp.push_back(node->val);
            q.pop();
            if (node->left != NULL)
                q.push(node->left);
            if (node->right != NULL)
                q.push(node->right);
        }
        res.push_back(temp);
    }
    reverse(res.begin(), res.end());
    return res;
}

二叉树的右视图

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
// 二叉树的右视图
vector<int> rightSideView(TreeNode* root) {
    queue<TreeNode*> node;
    vector<int> res;
    if (root == NULL)
        return res;
    node.push(root);
    while (!node.empty()) {
        int size = node.size();
        TreeNode* temp;
        for (int i = 0; i < size; ++i) {
            temp = node.front();
            node.pop();
            if (temp->left != NULL)
                node.push(temp->left);
            if (temp->right != NULL)
                node.push(temp->right);
        }
        res.push_back(temp->val);
    }
    return res;
}

二叉树的最大深度

递归

1
2
3
4
5
int maxDepth(TreeNode* root) {
    if (root == NULL)
        return 0;
    return 1+max(maxDepth(root->left), maxDepth(root->right));
}

非递归

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
int maxDepth(TreeNode* root) {
    queue<TreeNode*> q;
    if (root == NULL)
        return 0;
    q.push(root);
    int level = 0;
    while (!q.empty()) {
        int size = q.size();
        for (int i = 0; i < size; ++i) {
            if (q.front()->left != NULL)
                q.push(q.front()->left);
            if (q.front()->right != NULL)
                q.push(q.front()->right);
            q.pop();
        }
        ++level;
    }
    return level;
}

二叉树的最近公共组先

1
2
3
4
5
6
7
8
9
10
11
12
13
14
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
    if (root == NULL || root == p || root == q)
        return root;
    TreeNode* left = lowestCommonAncestor(root->left, p, q);
    TreeNode* right = lowestCommonAncestor(root->right, p, q);

    if (left == NULL)
        return right;
    if (right == NULL)
        return left;
    if (left && right)
        return root;
    return NULL;
}

平衡二叉树

暴力破解

1
2
3
4
5
6
7
8
9
10
11
12
13
14
int GetTreeDepth(TreeNode* root) {
    if (root == NULL)
        return 0;
    return 1 + max(GetTreeDepth(root->left), GetTreeDepth(root->right));
}

// 平衡二叉树
bool isBalanced(TreeNode* root) {
    if (root == NULL)
        return true;
    if (abs(GetTreeDepth(root->left) - GetTreeDepth(root->right)) > 1)
        return false;
    return isBalanced(root->left) && isBalanced(root->right);
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
int recur(TreeNode* node) {
    if (node == NULL)
        return 0;
    int left = recur(node->left);
    if (left == -1)
        return -1;
    int right = recur(node->right);
    if (right == -1)
        return -1;
    return abs(left-right) < 2 ? max(left, right) + 1 : -1;
}
bool isBalanced(TreeNode* root) {
    if (root == NULL)
        return true;
    return recur(root) != -1;
}

二叉搜索树的插入操作

递归

1
2
3
4
5
6
7
8
9
TreeNode* insertIntoBST(TreeNode* root, int val) {
    if (root == NULL)
        return new TreeNode(val);
    if (root->val > val)
        root->left = insertIntoBST(root->left, val);
    else
        root->right = insertIntoBST(root->right, val);
    return root;
}

迭代

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
TreeNode* insertIntoBST(TreeNode* root, int val) {
    TreeNode* node = root;
    if (root == NULL) {
        root = new TreeNode(val);
        return root;
    }
    while (node != NULL) {
        if (node->val > val) {
            if (node->left != NULL)
                node = node->left;
            else {
                node->left = new TreeNode(val);
                break;
            }
        } else if (node->val < val){
            if (node->right != NULL)
                node = node->right;
            else {
                node->right = new TreeNode(val);
                break;
            }
        }
        
    }
    return root;
}

恢复二叉搜索树

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
void recoverTree(TreeNode* root) {
    if (root == NULL)
        return;
    stack<TreeNode*> node;
    vector<TreeNode*> num;
    vector<int> swap;
    TreeNode* head = root;
    while (head != NULL || !node.empty()) {
        for (; head != NULL; head = head->left)
            node.push(head);
        num.push_back(node.top());
        head = node.top()->right;
        node.pop();
    }
    for (int i = 0; i < num.size() - 1; ++i) {
        if (num[i]->val > num[i+1]->val)
            swap.push_back(i);
    }
    if (swap.size() == 1) {
        int temp = num[swap[0]]->val;
        num[swap[0]]->val = num[swap[0]+1]->val;
        num[swap[0]+1]->val = temp;     
    } else {
        int temp = num[swap[0]]->val;
        num[swap[0]]->val = num[swap[1]+1]->val;
        num[swap[1]+1]->val = temp;
    }
}

不同的二叉搜索树2

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
vector<TreeNode*> generateTrees(int start, int n) {
    vector<TreeNode*> ans;
    if (start > n) return {NULL};
    for (int i = start; i <= n; ++i) {
        for (auto left : generateTrees(start, i - 1)) {
            for (auto right : generateTrees(i+1, n)) {
                TreeNode* root = new TreeNode(i, left, right);
                ans.push_back(root);
            }
        }
    }
    return ans;
}
vector<TreeNode*> generateTrees(int n) {
    if (n == 0) return {};
    return generateTrees(1, n);
}

二叉树的最大路径和

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
/**
 * 二叉树的最大路径和
 * @param root
 * @param sum
 * @return ret 当前结点最大路径和
 */
int maxPathSum(TreeNode* root, int &sum) {
    if (root == NULL)
        return 0;
    // 左结点最大路径和
    int left = max(maxPathSum(root->left, sum), 0);
    // 右节点最大路径和
    int right = max(maxPathSum(root->right, sum), 0);
    // 左节点+右节点+当前节点的路径和
    int lmr = root->val + left + right;
    sum = max(sum, lmr);
    // 返回当前节点可以连接父节点的最大值
    return root->val + max(left, right);
}
int maxPathSum(TreeNode* root) {
    int val = INT8_MIN;
    maxPathSum(root, val);
    return val;
}

数的子结构

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
bool recur(TreeNode* A, TreeNode* B) {
    if (B == NULL)
        return true;
    if (A == NULL || A->val != B->val)
        return false;
    return recur(A->left, B->left) && recur(A->right, B->right);
}
bool isSubStructure(TreeNode* A, TreeNode* B) {
    if (A == NULL || B == NULL)
        return false;
    bool root = recur(A, B);
    bool left = isSubStructure(A->left, B);
    bool right = isSubStructure(A->right, B);
    return root || left || right;
}

对称二叉树

1
2
3
4
5
6
7
8
9
10
11
12
13
14
bool isSymmetric(TreeNode* left, TreeNode* right) {
    if (left == NULL && right == NULL)
        return true;
    if (left == NULL || right == NULL)
        return false;
    if (left->val != right->val)
        return false;
    return isSymmetric(left->left, right->right) && isSymmetric(left->right, right->left);
}
bool isSymmetric(TreeNode* root) {
    if (root == NULL)
        return true;
    return isSymmetric(root->left, root->right);
}

二叉树中和为某一值的路径

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
void pathSum(TreeNode* root, vector<vector<int>>& res, vector<int>& temp, int sum) {
    if (root == NULL) {
        return;
    }
    temp.push_back(root->val);
    if (root->val == sum && root->left == NULL && root->right == NULL)
        res.push_back(temp);
    pathSum(root->left, res, temp, sum-root->val);
    pathSum(root->right, res, temp, sum-root->val);
    temp.pop_back();
}
vector<vector<int>> pathSum(TreeNode* root, int sum) {
    vector<vector<int>> res;
    if (root == NULL)
        return res;
    vector<int> tmp;
    pathSum(root, res, tmp, sum);
    return res;
}

二叉树与双向链表

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class solution {
public:
    Node* treeToDoublyList(Node* root) {
        if (root == NULL) return NULL;
        dfs(root);
        head->left = pre;
        pre->right = head;
        return head;
    }
private:
    Node *pre, *head;
    void dfs(Node* cur) {
        if (cur == NULL) return;
        dfs(cur->left);
        if (pre != NULL) pre->right = cur;
        else head = cur;
        cur->left = pre;
        pre = cur;
        dfs(cur->right);
    }
}

图结构

图结构中数据元素之间存在着“多对多”的关系。

广度优先

堆

数据流中的中位数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class MedianFinder {
public:
    MedianFinder() {}
    void addNum(int num) {
        if (A.size() != B.size()) {
            A.push(num);
            B.push(A.top());
            A.pop();
        } else {
            B.push(num);
            A.push(B.top());
            B.pop();
        }
    }
    double findMedian() {
        return A.size() != B.size() ? A.top() : (A.top() + B.top()) / 2.0;
    }
private:
    priority_queue<int, vector<int>, greater<int>> A;
    priority_queue<int, vector<int>, less<int>> B;
};

算法

查找和排序

二分查找框架

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
int binarySearch(vector<int> nums, int target) {
    int left = 0, right = ...;

    while(...) {
        int mid = left + (right - left) / 2;
        if (nums[mid] == target) {
            ...
        } else if (nums[mid] < target) {
            left = ...
        } else if (nums[mid] > target) {
            right = ...
        }
    }
    return ...;
}

在排序数组中查找元素的第一个和最后一个位置

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
vector<int> searchRange(vector<int>& nums, int target) {
    vector<int> res;
    int left = 0, right = nums.size() - 1;
    while (left <= right) {
        int mid = left + (right - left) / 2;
        if (nums[mid] >= target) right = mid - 1;
        else left = mid + 1;  
    }
    if (left >= nums.size() || nums[left] != target) res.push_back(-1);
    else res.push_back(left);

    right = nums.size() - 1;
    while (left <= right) {
        int mid = left + (right - left) / 2;
        if (nums[mid] <= target) left = mid + 1;
        else right = mid - 1;
    }
    if (right < 0 || nums[right] != target) res.push_back(-1);
    else res.push_back(right);
    return res;
}

顺序查找

1
2
3
4
5
6
7
int search(Student *stu, int n, int  key) {
    for (int i = 0; i < n; ++i) {
        if (stu[i].id == key)
            return i;
    }
    return -1;
}

折半查找

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
/**
 * 折半查找
 * @param key 关键字顺序表
 * @param n 记录个数
 * @param k 要查找的关键字
 * @return
 */
int bin_search(int *key, int n, int k) {
    int low = 0, high = n - 1, mid;
    while (low <= high) {
        mid = (low + high) / 2;
        if (key[mid] == k)
            return mid;
        if (k > key[mid])
            low = mid + 1;
        else if (k < key[mid])
            high = mid - 1;
    }
    return -1;
}

请实现有重复数字的有序数组的二分查找。
输出在数组中第一个大于等于查找值的位置，如果数组中不存在这样的数，则输出数组长度加一。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
int bin_search(int n, int v, vector<int>& a) {
    int left = 0;
    int right = n - 1;
    int mid;
    while (left <= right) {
        mid = (left + right) / 2;
        if (a[mid] >= v) {
            if (mid == 0 || a[mid-1] < v)
                return mid + 1;
            else
                right = mid - 1;
        }
        else
            left = mid + 1;
    }
    return n + 1;
}

直接插入排序

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
/**
 * 直接插入排序
 * @param arr 数组
 * @param n 数组元素个数
 */
void insertSort(int arr[], int n) {
    for (int i = 1; i < n; ++i) {
        int temp = arr[i];
        int j = i - 1;
        // for (j; j >= 0; --j) {
        //     if (temp < arr[j]) {
        //         arr[j + 1] = arr[j];
        //     } else {
        //         break;
        //     }
        // }
        // arr[j + 1] = temp;

        while (j >= 0 && temp < arr[j]) {
            arr[j+1] = arr[j];
            j--;
        }
        arr[j+1] = temp;
    }
}

选择排序

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
/**
 * 选择排序
 * @param arr 数组
 * @param n 数组元素个数
 */
void selectSort(int arr[], int n) {
    for (int i = 0; i < n; ++i) {
        int min = i, temp;
        for (int j = i; j < n; ++j) {
            if (arr[j] < arr[min])
                min = j;
        }
        if (min != i) {
            temp = arr[min];
            arr[min] = arr[i];
            arr[i] = temp;
        }
    }
}

冒泡排序

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
/**
 * 冒泡排序
 * 添加标志变量flag，进行交换flag为真，可以进入下一循环，为进行交换flag为假（数据已有序，无须再进行交换）循环终止。
 * @param arr 数组
 * @param n 数组元素个数
 */
void BubbleSort(int arr[], int n) {
    bool flag = true;
    for (int i = 0; i < n && flag; ++i) {
        flag = false;
        for (int j = 0; j < n - i - 1; ++j) {
            if (arr[j] > arr[j + 1]) {
                flag = true;
                int temp = arr[j];
                arr[j] = arr[j + 1];
                arr[j + 1] = temp;
            }
        }
    }
}

希尔排序

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
/**
 * 希尔排序
 * 使用do-while是因为flag为2时已经有序，但是flag为1时不是有序的。
 * @param arr 数组
 * @param n 数组元素个数
 */
void shellSort(int arr[], int n) {
    int i, j, gap = n;
    bool flag = true;
    int temp;
    while(gap > 1) {
        gap = gap / 2;
        do {
            flag = false;
            for (i = 0; i < n - gap; ++i) {
                j = i + gap;
                if (arr[i] > arr[j]) {
                    temp = arr[i];
                    arr[i] = arr[j];
                    arr[j] = temp;
                    flag = true;
                }
            }
        } while(flag);
    }
}

快速排序

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
void swap(int &a, int &b) {
    int temp = a;
    a = b;
    b = temp;
}

void quick(int arr[], int start, int end) {
    if (start >= end)
        return;
    int left = start, right = end, key = arr[start];
    // 进行循环，将小于基准元素的元素放到左边，大于基准元素的元素放到右边
    while (left < right) {
        while(left < right && arr[right] >= key)
            right--;
        while(left < right && arr[left] <= key)
            left++;
        swap(arr[left], arr[right]);
        // for (int i = 0; i < 10; ++i) {
        //     cout << arr[i] << ' ';
        // }
        // cout << endl;
    }
    // 交换基准元素与left的位置，循环中先从右开始，因此left和right相等的位置为小于基准元素的值
    swap(arr[start], arr[left]);
    quick(arr, start, left - 1);
    quick(arr, left + 1, end);
}
/**
 * 快速排序
 * @param arr 数组
 * @param n 数组元素个数
 */
void quickSort(int arr[], int n) {
    quick(arr, 0, n - 1);
}

循环实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
int Partition(int *arr, int start, int end) {
    if (start == end)
        return start;
    int left = start, right = end, key = arr[start];
    while (left < right) {
        while (left < right && arr[right] >= key)
            right--;
        arr[left] = arr[right];
        while (left < right && arr[left] <= key)
            left++;
        arr[right] = arr[left];
    }
    arr[left] = key;
    return left;
}
/**
 * 非递归实现快排
 */
void quickSort2(int arr[], int n) {
    stack<int> st;
    st.push(0);
    st.push(n-1);
    while (!st.empty()) {
        int right = st.top();
        st.pop();
        int left = st.top();
        st.pop();
        int mid = Partition(arr, left, right);
        if (mid - 1 > left) {
            st.push(left);
            st.push(mid - 1);
        }
        if (mid + 1 < right) {
            st.push(mid + 1);
            st.push(right);
        }
    }
}

堆排序

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
/**
 * 调整大顶堆
 * @param arr
 * @param i
 * @param len
 */
void adjust(int arr[], int i, int len) {
    int temp = arr[i];
    // 从i结点的左子结点开始，也就是2i+1
    for (int k = 2 * i + 1; k < len; k = k * 2 + 1) {
        // 如果左子结点小于右子结点，k指向右子结点
        if (k + 1 < len && arr[k] < arr[k + 1])
            k++;
        // 如果子结点大于父节点，将子结点的值赋给父节点
        if (arr[k] > temp) {
            arr[i] = arr[k];
            i = k;
        } else {
            break;
        }
    }
    arr[i] = temp;
}

/**
 * 堆排序
 * @param arr 数组
 * @param n 数组元素个数
 */
void headSort(int arr[], int n) {
    int i, temp;
    // 1.构建大顶堆
    for (i = n / 2; i >= 0; --i) {
        // 从第一个非叶子结点从下至上，从右至左调整结构
        adjust(arr, i, n);
    }
    // 2.调整堆结构并交换堆顶元素与末尾元素
    for (int j = n - 1; j > 0; --j) {
        swap(arr[0], arr[j]);
        adjust(arr, 0, j);
    }
}

归并排序

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
/**
 * 归并排序
 * @param arr 数组
 * @param n 数组元素个数
 */
class MergeSort {
public:
    MergeSort(vector<int>& arr) {
        sort(arr, 0, arr.size()-1);
    }
    ~MergeSort();
private:
    void merge(vector<int>& arr, int start, int mid, int end) {
        vector<int> left(arr.begin()+start, arr.begin()+mid+1);
        vector<int> right(arr.begin()+mid+1, arr.begin()+end+1);
        int cur = start;
        for (int i = 0, j = 0; i < left.size(), j < right.size();) {
            if (left[i] < right[j]) {
                arr[cur++] = left[i++];
            } else {
                arr[cur++] = right[j++];
            }
            if (i == left.size()) {
                for (j; j < right.size();++j) arr[cur++] = right[j];
                break;
            }
            if (j == right.size()) {
                for (i; i < left.size();++i) arr[cur++] = left[i];
                break;
            }
        }
    }
    void sort(vector<int>& arr, int start, int end) {
        if (start >= end) return;
        int mid = start + (end - start) / 2;
        sort(arr, start, mid);
        sort(arr, mid+1, end);
        merge(arr, start, mid, end);
    }
};

矩阵中的路径

DFS用栈维护， BFS用队列维护

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
bool dfs(vector<vector<char>>& board, string& word, int i, int j, int k) {
    if (i >= board.size() || j >= board[0].size() || i < 0 || j < 0 || board[i][j] != word[k])
        return false;
    if (k == word.size() - 1) return true;
    char temp = board[i][j];
    board[i][j] = '\0';
    if (dfs(board, word, i+1, j, k+1) || dfs(board, word, i-1, j, k+1) ||
        dfs(board, word, i, j+1, k+1) || dfs(board, word, i, j-1, k+1) )
                    return true;
    board[i][j] = temp;
    return false;
}
bool exist(vector<vector<char>>& board, string word) {
    for (int i = 0; i < board.size(); ++i) {
        for (int j = 0; j < board[0].size(); ++j)
            if (dfs(board, word, i, j, 0)) 
                return true;
    }
    return false;
}

把数组排成最小的数

1
2
3
4
5
6
7
8
9
10
11
12
string minNumber(vector<int> &nums) {
    string res;
    vector<string> strs;
    for (auto a:nums) {
        strs.push_back(to_string(a));
    }
    sort(strs.begin(), strs.end(), [](string &x, string &y) {return x+y < y+x;});
    for (auto a:strs) {
        res += a;
    }
    return res;
}

扑克牌中的顺子

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
bool isStraight(vector<int> &nums) {
    sort(nums.begin(), nums.end());
    int flag = 0;
    for (int i = 0; i < nums.size()-1; ++i) {
        if (nums[i] == 0) {
            flag++;
            continue;
        }
        if (nums[i]+1 == nums[i+1])
            continue;
        else if (nums[i] == nums[i+1])
            return false;
        else {
            flag -= nums[i+1] - nums[i] - 1;
        }
        if (flag < 0)
            return false;
    }
    return true;
}
1
2
3
4
5
6
7
8
9
10
11
12
bool isStraight(vector<int> &nums) {
    unordered_set<int> repeat;
    int maxNum = 0, minNum = 14;
    for (int num:nums) {
        if (num == 0) continue;
        maxNum = max(maxNum, num);
        minNum = min(minNum, num);
        if (repeat.find(num) != repeat.end()) return false;
        repeat.insert(num);
    }
    return maxNum - minNum < 5;
}

数组中重复的数字

1
2
3
4
5
6
7
8
int findRepeatNumber(vector<int>& nums) {
    unordered_set<int> repeat;
    for (int num:nums) {
        if (repeat.find(num) != repeat.end()) return num;
        repeat.insert(num);
    }
    return -1;
}
1
2
3
4
5
6
7
8
int findRepeatNumber(vector<int> &nums) {
    unordered_map<int , bool> map;
    for (int num : nums) {
        if (map[num]) return num;
        map[num] = true;
    }
    return -1;
}

二维数组中的查找

1
2
3
4
5
6
7
8
9
10
11
12
bool findNumberIn2DArray(vector<vector<int>> &matrix, int target) {
    int i = matrix.size() - 1, j = 0;
    while (i >=0 && j < matrix[0].size()) {
        if (matrix[i][j] == target)
            return true;
        else if (matrix[i][j] > target)
            i--;
        else
            j++;
    }
    return false;
}

旋转数组的最小数字

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
int minArray(vector<int> &numbers) {
    int end = numbers.size() - 1;
    int start = 0;
    while (start < end) {
        int mid = (end + start) / 2;
        if (numbers[mid] < numbers[end]) {
            end = mid;
        } else if (numbers[mid] > numbers[end]){
            start = mid + 1;
        } else {
            end--;
        }
    }
    return numbers[start];
}

第一个只出现一次的数字

1
2
3
4
5
6
7
8
char firstUniqChar(string s)  {
    unordered_map<char, bool> dic;
    for (char a : s)
        dic[a] = dic.find(a) == dic.end();
    for (char c : s)
        if (dic[c]) return c;
    return ' ';
}
1
2
3
4
5
6
7
8
9
10
11
12
13
char firstUniqChar(string s) {
    vector<char> keys;
    unordered_map<char, bool> dic;
    for (char c : s) {
        if (dic.find(c) == dic.end())
            keys.push_back(c);
        dic[c] = dic.find(c) == dic.end();
    }
    for (char c : keys) {
        if (dic[c]) return c;
    }
    return ' ';
}

在排序数组中查找数字

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
int search(vector<int> &nums, int target) {
    int i = 0, j = nums.size() - 1;
    while (i <= j) {
        int mid = (i + j) / 2;
        if (nums[mid] <= target) i = mid + 1;
        else j = mid - 1;
    }
    int right = i;
    if (j >= 0 && nums[j] != target) return 0;
    i = 0, j = nums.size() - 1;
    while (i <= j) {
        int mid = (i + j) / 2;
        if (nums[mid] < target) i = mid + 1;
        else j = mid - 1;
    }
    int left = j;
    return right - left - 1;
}

0~n-1中缺失的数字

1
2
3
4
5
6
7
8
9
int missingNumber(vector<int> &nums) {
    int start = 0, end = nums.size() - 1;
    while (start <= end) {
        int mid = (start + end) / 2;
        if (nums[mid] > mid) end = mid - 1;
        else start = mid + 1;
    }
    return start+1;
}

回溯

算法框架

1
2
3
4
5
6
7
8
9
10
result = []
def backtrack(路径, 选择列表):
    if 满足结束条件:
        result.add(路径)
        return

    for 选择 in 选择列表:
        做选择
        backtrack(路径, 选择列表)
        撤销选择

四皇后问题

在一个4×4的国际象棋棋盘上，一次一个地摆放4枚皇后棋子，摆好后满足每行、每列和对角线上只允许出现一枚棋子，即棋子间不许相互俘获。

解决策略：

  1. 初始化一个4x4的数组Q，Q[i][j]=1表示该点有皇后，无皇后的点置为0。
  2. 遍历每一行，使用isCorrect判断当前点是否可以放置皇后，可以放置后使用递归将皇后数量+1
  3. 确定四个皇后之后将上个确定的皇后置为0进行回溯，继续执行循环。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
// 判断皇后是否可以放置到[i][j]
int isCorrect(int i, int j, int (*QueenArray)[4]) {
    int s, t;
    // 判断行
    for (s = i, t = 0; t < 4; ++t)
        if (QueenArray[s][t] == 1 && t != j)
            return 0;
    // 判断列
    for (s = 0, t = j; s < 4; ++s)
        if (QueenArray[s][t] == 1 && s != i)
            return 0;
    // 判断左上
    for (s = i - 1, t = j - 1; s >= 0 && t >= 0; s--, t--)
        if (QueenArray[s][t] == 1)
            return 0;
    // 判读右上
    for (s = i - 1, t = j + 1; s >= 0 && t < 4; s--, t++)
        if (QueenArray[s][t] == 1)
            return 0;
    // 判断左下
    for (s = i + 1, t = j - 1; s < 4 && t >= 0; s++, t--)
        if (QueenArray[s][t] == 1)
            return 0;
    // 判读右下
    for (s = i + 1, t = j + 1; s < 4 && t < 4; s++, t++)
        if (QueenArray[s][t] == 1)
            return 0;
    
    return 1;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
/**
 * 回溯法解决4皇后问题
 * @param queenNum 当前皇后数量
 * @param QueenArray 皇后数组
 */
void Queen(int queenNum, int (*QueenArray)[4]) {
    int i, k;
    // 四个皇后都确定
    if (queenNum == 4) {
        for (i = 0; i < 4; i++) {
            for (k = 0; k < 4; k++)
                cout << QueenArray[i][k] << ' ';
            cout << endl;
        }
        cout << endl;
        count++;
        return;
    }
    for (i = 0; i < 4; i++) {
        if (isCorrect(i, queenNum, QueenArray)) {
            QueenArray[i][queenNum] = 1;
            Queen(queenNum+1, QueenArray);
            QueenArray[i][queenNum] = 0;
        }
    }
}

动态规划

算法框架

1
2
3
4
5
6
7
# 初始化 base case
dp[0][0][...] = base
# 进行状态转移
for 状态1 in 状态1的所有取值：
    for 状态2 in 状态2的所有取值：
        for ...
            dp[状态1][状态2][...] = 求最值(选择1，选择2...)

上台阶问题

有一楼梯共m级，若每次只能跨上一级或二级，要走上第m级，共有多少走法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
/**
 * 上台阶问题
 * @param n 台阶数
 * @return
 */
int UpStairs(int n) {
    if (n < 0)
        return -1;
    if (n == 1)
        return 1;
    if (n == 2)
        return 2;
    return UpStairs(n - 1) + UpStairs(n - 2);
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
// 使用动态规划解决
int UpStairs(int n) {
    if (n < 0)
        return -1;
    if (n == 1)
        return 1;
    if (n == 2)
        return 2;
    int *dp = new int[n+1];
    dp[0] = 0;
    dp[1] = 1;
    dp[2] = 2;
    for (int i = 3; i <= n; ++i)
        dp[i] = dp[i-1] + dp[i-2]
    return dp[n];
}

编辑距离

已知两个字符串word1和word2，求从word1转化成word2最少需要几步。其中，每一步只能进行以下三个操作之一：

  • 插入一个字符
  • 删除一个字符
  • 替换一个字符

解决策略：

  1. 使用一个二维数组dp记录需要的操作数
  2. dp[i][j]表示word1转化为word2需要的最小操作数，有两种状态，word1[i]==word2[j]和word1[i]!=word2[j]，
    • word1[i] == word2[j]，则dp[i][j] = dp[i-1][j-1]，
    • word1[i] !=wrod2[j]，有三条路径：
      1. 比如，”xyz” => “efg” 的最小编辑距离等于 “xy” => “efg” 的最小编辑距离 + 1（因为允许插入操作，插入一个 “z”），抽象的描述便是 d[m][n] === d[m-1][n] + 1。
      2. 比如，”xyz” => “efg” 的最小编辑距离等于 “xyzg” => “efg” 的最小编辑距离 + 1，且因为最后一个字符都是 “g”，根据第一个判断条件，可以再等于 “xyz” => “ef” 的最小编辑距离 + 1，因此，得到结论：”xyz” => “efg” 的最小编辑距离等于 “xyz” => “ef” 的最小编辑距离 + 1，抽象的描述便是：d[m][n] === d[m][n-1] + 1。
      3. 比如，”xyz” => “efg” 的最小编辑距离等于 “xyg” => “efg” 的最小编辑距离 + 1（因为允许替换操作，可以把 “g” 换成 “z”），再等于 “xy” => “ef” 的编辑距离 + 1（根据第一个判断条件），抽象的描述便是： d[m][n] === d[m-1][n-1] + 1。
        上述三种情况都有可能出现，因此，取其中的最小值便是整体上的最小编辑距离。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
/**
 * 编辑距离
 */
int miniDistance(string word1, string word2) {
    int n1 = word1.size();
    int n2 = word2.size();
    // vector <vector <int>> dp[n1][n2];
    // 开辟空间
    int **dp = new int*[n1+1];
    for (int i = 0; i <= n1; ++i)
        dp[i] = new int[n2+1]();
    // 初始化
    for (int i = 0; i < n1; ++i)
        dp[i+1][0] = dp[i][0] + 1;
    for (int i = 0; i < n2; ++i)
        dp[0][i+1] = dp[0][i] + 1;
    
    for  (int i = 1; i <= n1; ++i) {
        for (int j = 1; j <= n2; ++j)
            if (word1[i-1] == word2[j-1])
                dp[i][j] = dp[i-1][j-1];
            else 
                dp[i][j] = min(min(dp[i-1][j-1], dp[i-1][j]), dp[i][j-1]) + 1;
    }
    // 释放空间
    for (int i = 0; i < n1; ++i)
        delete[] dp[i];
    delete[] dp;

    return dp[n1][n2];
}

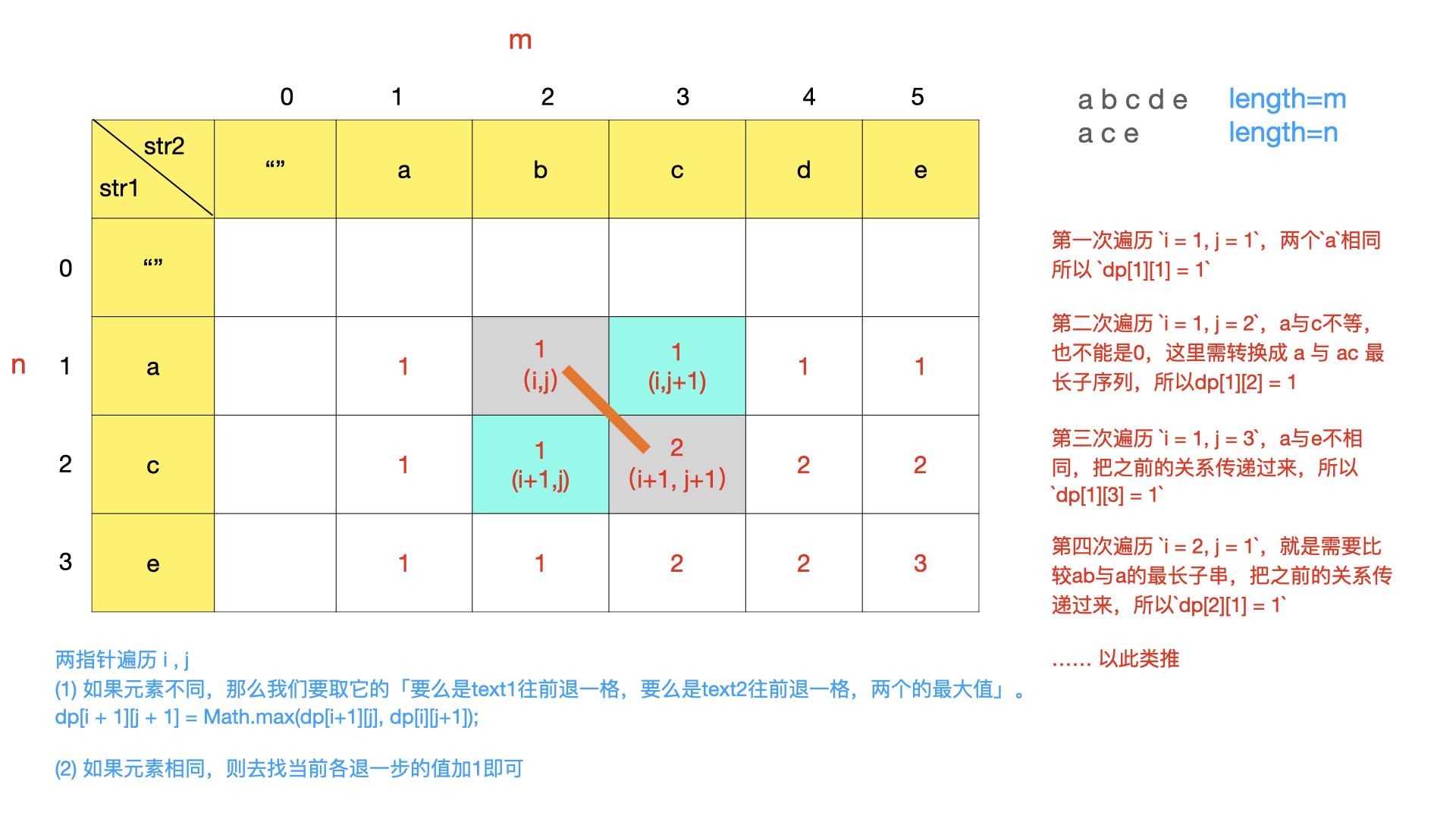
最长公共子序列

最长公共子序列

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
int longestCommonSubsequence(string text1, string text2) {
    if (text1.empty() || text2.empty())
        return 0;
    int m = text1.size(), n = text2.size();
    vector<vector<int>> dp(m + 1, vector<int>(n + 1));
    for (int i = 1; i <= m; ++i) {
        for (int j = 1; j <= n; ++j) {
            if (text1[i-1] == text2[j-1])
                dp[i][j] = 1 + dp[i-1][j-1];
            else
                dp[i][j] = max(dp[i-1][j], dp[i][j-1]);
        }
    }
    return dp[m][n];
}

最长回文子序列

1
2
3
4
5
6
7
8
9
10
11
12
13
int longestPalindromeSubseq(string s) {
    int len = s.size();
    vector<vector<int>> dp(len+1, vector<int>(len+1));
    for (int i = 0; i < len; ++i) {
        for (int j = 0; j < len; ++j) {
            if (s[i] == s[len-1-j])
                dp[i+1][j+1] = 1 + dp[i][j];
            else
                dp[i+1][j+1] = max(dp[i][j+1], dp[i+1][j]);
        }
    }
    return dp[len][len];
}

完全平方数

递归

1
2
3
4
5
6
7
8
9
10
11
12
13
int minNumSquares(int n) {
    if (n == 0)
        return 0;
    int count = INT32_MAX;
    for (int i = 1; i * i <= n; ++i)
        count = min(count, minNumSquares(n - i * i) + 1);
    return count;
}

// 完全平方数
int numSquares(int n) {
    return minNumSquares(n);
}

非递归

1
2
3
4
5
6
7
8
9
int numSquares(int n) {
    vector<int> dp(n+1, n+1);
    dp[0] = 0;
    for (int i = 1; i <= n; ++i) {
        for (int j = 1; j * j <= i; ++j)
            dp[i] = min(dp[i], dp[i-j*j] + 1);
    }
    return dp[n];
}

杨辉三角2

1
2
3
4
5
6
7
8
vector<int> getRow(int rowIndex) {
    vector<int> res(rowIndex+1, 1);
    for (int i = 2; i < rowIndex+1; ++i) {
        for (int j = i - 1 ; j > 0; j--)
            res[j] = res[j-1] + res[j];
    }
    return res;
}

计算平方数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
double quickMul(double x, long long N) {
    double ans = 1.0;
    while (N > 0) {
        if (N & 1 == 1)
            ans *= x;
        x *= x;
        N = N >> 1;
    }
    return ans;
}
double quickMul(double x, long long n) {
    if (n == 0)
        return 1.0;
    double half = quickMul(x, n / 2);
    if (n % 2 == 0)
        return half * half;
    else
        return half * half * x;
}
double myPow(double x, int n) {
    long long N = n;
    return N >= 0 ? quickMul(x, N) : 1.0 / quickMul(x, -N);
}

第k个语法符号

1
2
3
4
5
int kthGrammar(int N, int K) {
    if (N == 1)
        return 0;
    return kthGrammar(N - 1, (K + 1) / 2) == 0 ? (1 - (K % 2)) : (K % 2);
}

礼物的最大价值

1
2
3
4
5
6
7
8
9
10
11
12
13
int maxValue(vector<vector<int>> &grid) {
    if (grid.empty())
        return 0;
    int m = grid.size();
    int n = grid[0].size();
    vector<vector<int>> dp(m+1, vector<int>(n+1));
    for (int i = 1; i <= m; ++i) {
        for (int j = 1; j <= n; ++j) {
            dp[i][j] = max(dp[i-1][j], dp[i][j-1]) + grid[i-1][j-1];
        }
    }
    return dp[m][n];
}

股票的最大利润

  • 一次购买
    1
    2
    3
    4
    5
    6
    7
    8
    int maxProfit(vector<int>& prices) {
        int cost = INT32_MAX, profit = 0;
        for (int price : prices) {
            cost = min(cost, price);
            profit = max(profit, price-cost);
        }
        return profit;
    }

  • 买卖股票的最佳时机二

    1
    2
    3
    4
    5
    6
    7
    8
    int maxProfit(vector<int>& prices) {
        int profit = 0;
        for (int i = 1; i < prices.size(); ++i) {
            if (prices[i] > prices[i-1])
                profit += prices[i] - prices[i-1];
        }
        return profit;
    }

  • 买卖股票的最佳时机三

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    int maxProfit(vector<int>& prices) {
        int days = prices.size();
        vector<vector<vector<int>>> dp(days, vector<vector<int>>(3, vector<int>(2)));
        for (int i = 0; i < days; ++i)
            for (int j = 0; j < 3; ++j) {
                if (i - 1 == -1) {
                    dp[i][j][0] = 0;
                    dp[i][j][1] = -prices[i];
                    continue;
                }
                if (j == 0) {
                    dp[i][j][0] = 0;
                    dp[i][j][1] = max(dp[i-1][0][1], dp[i-1][0][0]-prices[i]);
                    continue;
                }
                dp[i][j][0] = max(dp[i-1][j][0], dp[i-1][j][1] + prices[i]);
                dp[i][j][1] = max(dp[i-1][j][1], dp[i-1][j-1][0]-prices[i]);
            }
        return dp[days-1][2][0];
    }

  • 买卖股票的最佳时机四

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    35
    int maxProfit(vector<int>& prices) {
        int n = prices.size();
        int dp_i_0 = 0, dp_i_1 = -prices[0];
        for (int i = 0; i < n; ++i) {
            int temp = dp_i_0;
            dp_i_0 = max(dp_i_0, dp_i_1 + prices[i]);
            dp_i_1 = max(dp_i_1, temp-prices[i]);
        }
        return dp_i_0;
    }
    int maxProfit(int k, vector<int>& prices) {
        int days = prices.size();
        if (k == 0)
            return 0;
        if (k > days/2)
            maxProfit(prices);
        vector<vector<vector<int>>> dp(days, vector<vector<int>>(k+1, vector<int>(2)));
        for (int i = 0; i < days; ++i) {
            for (int j = 0; j <= k; ++j) {
                if (i - 1 == -1) {
                    dp[i][j][0] = 0;
                    dp[i][j][1] = -prices[i];
                    continue;
                }
                if (j == 0) {
                    dp[i][j][0] = 0;
                    dp[i][j][1] = max(dp[i-1][0][1], dp[i-1][0][0]-prices[i]);
                    continue;
                }
                dp[i][j][0] = max(dp[i-1][j][0], dp[i-1][j][1] + prices[i]);
                dp[i][j][1] = max(dp[i-1][j][1], dp[i-1][j-1][0]-prices[i]);
            }
        }
        return dp[days-1][k][0];
    }

打家劫舍

  • 打家劫舍1
1
2
3
4
5
6
7
8
9
10
11
12
int rob(vector<int>& nums) {
    int n = nums.size();
    if (n == 0) return 0;
    if (n == 1) return nums[0];
    int dp_i_1 = 0, dp_i_2 = 0, dp_i = 0;
    for (int i = n-1; i >= 0; i--) {
        dp_i = max(dp_i_1, dp_i_2 + nums[i]);
        dp_i_2 = dp_i_1;
        dp_i_1 = dp_i;
    }
    return dp_i;
}
  • 打家劫舍2
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
public:
    int rob(vector<int>& nums) {
        int n = nums.size();
        if (n == 1) return nums[0];
        return max(dp(nums, 0, n-1), dp(nums, 1, n));
    }
private:
    int dp(vector<int>& nums, int start ,int end) {
        int dp_i = 0, dp_i_1 = 0, dp_i_2 = 0;
        for (int i = start; i < end; ++i) {
            dp_i = max(dp_i_1, dp_i_2 + nums[i]);
            dp_i_2 = dp_i_1;
            dp_i_1 = dp_i;
        }
        return dp_i;
    }
};
  • 打家劫舍3
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
public:
    int rob(TreeNode* root) {
        if (root == NULL) return 0;
        if (memo.find(root) != memo.end()) return memo[root];
        int do_it = root->val + (root->left == NULL ? 0 : rob(root->left->left)+rob(root->left->right))
                     + (root->right == NULL ? 0 : rob(root->right->left) + rob(root->right->right));
        int not_do = rob(root->left) + rob(root->right);
        int res = max(do_it, not_do);
        memo[root] = res;
        return res;
    }
private:
    unordered_map<TreeNode*, int> memo;
};

BFS

算法框架

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
// 计算从起点 start 到终点 target 的最近距离
int BFS(Node start, Node target) {
    queue<Node> q; // 核心数据结构
    set<Node> visited; // 避免走回头路

    q.offer(start); // 将起点加入队列
    visited.add(start);
    int step = 0; // 记录扩散的步数

    while (q not empty) {
        int sz = q.size();
        /* 将当前队列中的所有节点向四周扩散 */
        for (int i = 0; i < sz; i++) {
            Node cur = q.poll();
            /* 划重点：这里判断是否到达终点 */
            if (cur is target)
                return step;
            /* 将 cur 的相邻节点加入队列 */
            for (Node x : cur.adj())
                if (x not in visited) {
                    q.offer(x);
                    visited.add(x);
                }
        }
        /* 划重点：更新步数在这里 */
        step++;
    }
}

二叉树的最小深度

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
int minDepth(TreeNode* root) {
    queue<TreeNode*> nodes;
    int depth = 1;
    if (root == NULL) return 0;
    nodes.push(root);
    while (!nodes.empty()) {
        int size = nodes.size();
        for (int i = 0; i < size; ++i) {
            if (nodes.front()->left == NULL && nodes.front()->right == NULL) return depth;
            if (nodes.front()->left != NULL) nodes.push(nodes.front()->left);
            if (nodes.front()->right != NULL) nodes.push(nodes.front()->right);
            nodes.pop();
        }
        depth++;
    }
    return depth;
}

打开转盘锁

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
string plusUp(string str, int i) {
    string s = str;
    if (s[i] == '9') s[i] = '0';
    else s[i] += 1;
    return s;
}
string plusDown(string str, int i) {
    string s = str;
    if (s[i] == '0') s[i] = '9';
    else s[i] -= 1;
    return s;
}

int openLock(vector<string>& deadends, string target) {
    queue<string> q;
    // 记录死亡密码
    unordered_set<string> deads;
    deads.insert(deadends.begin(), deadends.end());
    // 记录已经穷举过的密码
    unordered_set<string> visited;
    q.push("0000");
    visited.insert("0000");
    int step = 0;
    while (!q.empty()) {
        int size = q.size();
        for (int i = 0; i < size; ++i) {
            string temp = q.front();
            q.pop();
            if (deads.find(temp) != deads.end()) continue;
            if (temp == target) return step;
            // 遍历相邻节点
            for (int j = 0; j < 4; ++j) {
                string up = plusUp(temp, j);
                if (visited.find(up) == visited.end()) {
                    q.push(up);
                    visited.insert(up);
                }
                string down = plusDown(temp, j);
                if (visited.find(down) == visited.end()) {
                    q.push(down);
                    visited.insert(down);
                }
            }
        }
        step++;
    }
    return -1;
}

贪心

二叉搜索树的后序遍历序列

1
2
3
4
5
6
7
8
9
10
11
bool recur(vector<int> postorder, int start, int end) {
    if (start >= end) return true;
    int p = start;
    while (postorder[p] < postorder[end]) p++;
    int m = p;
    while (postorder[p] > postorder[end]) p++;
    return p==end && recur(postorder, start, m-1) && recur(postorder, m, end-1);
}
bool verifyPostorder(vector<int>& postorder) {
    return recur(postorder, 0, postorder.size()-1);
}

滑动窗口问题

算法框架

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
void slidingWindow(string s, string t) {
    unordered_map<char, int> need, window;
    for (char c : t) need[c]++;

    int left = 0, right = 0;
    int valid = 0;
    while (right < s.size()) {
        // c是将移入窗口的字符
        char c = s[right];
        // 右移窗口
        right++;
        // 进行窗口数据更新
        ...
        // *** debug 输出位置 ***
        printf("window: [%d, %d]\n", left, right);
        /****************************/

        // 判断左窗口是否要收缩
        while (window needs shrink) {
            // d是将要移出窗口的字符
            char d = s[left];
            // 左移窗口
            left++;
            // 进行窗口内数据的一系列更新
            ...
        }
    }
}

最长不含重复字符的子字符串

使用无序集合unordered_set保存子串并检验是否有重复字符

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
int lengthOfLongestSubstring(string s) {
    if (s.size() == 0) return 0;
    unordered_set<char> dp;
    int maxStr = 0;
    int left = 0;
    for (int i = 0; i < s.size(); ++i) {
        while (dp.find(s[i]) != dp.end()) {
            dp.erase(s[left]);
            left++;
        }
        maxStr = max(maxStr, i-left+1);
        dp.insert(s[i]);
    }
    return maxStr;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
int lengthOfLongestSubstring(string s) {
    unordered_map<char, int> window;
    int res = 0;
    int left = 0, right = 0;
    while (right < s.size()) {
        char c = s[right];
        right++;
        window[c]++;
        
        while (window[c] > 1) {
            char d = s[left];
            left++;
            window[d]--;
        }
        res = max(res, right - left);
    }
    return res;
}

最小子串覆盖

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
string minWindow(string s, string t) {
    unordered_map<char, int> need, window;
    for (char c : t) need[c]++;
    int left = 0, right = 0;
    int valid = 0;
    // 记录最小覆盖子串的起始索引及长度
    int start = 0, len = INT32_MAX;
    while (right < s.size()) {
        char c = s[right];
        right++;
        if (need.count(c)) {
            window[c]++;
            if (window[c] == need[c])
                valid++;
        }

        while (valid == need.size()) {
            if (right - left < len) {
                start = left;
                len = right - left;
            }
            char d = s[left];
            left++;
            if (need.count(d)) {
                if (window[d] == need[d])
                    valid--;
                window[d]--;
            }
        }
    }
    return len == INT32_MAX ? "" : s.substr(start, len);
}

字符串的排列

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
bool checkInclusion(string s1, string s2) {
    unordered_map<char, int> need, window;
    for (char a : s1) need[a]++;

    int left = 0, right = 0;
    int valid = 0;
    while (right < s2.size()) {
        char c = s2[right];
        right++;
        if (need.count(c)) {
            window[c]++;
            if (window[c] == need[c])
                valid++;
        }

        while (right - left >= s1.size()) {
            if (valid == need.size()) return true;
            char d = s2[left];
            left++;
            if (need.count(d)) {
                if (window[d] == need[d]) valid--;
                window[d]--;
            }
        }
    }
    return false;
}

找到字符串中索引字母异位词

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
vector<int> findAnagrams(string s, string p) {
    unordered_map<char, int> need, window;
    for (char a : p) need[a]++;
    vector<int> res;
    
    int left = 0, right = 0;
    int valid = 0;
    while (right < s.size()) {
        char c = s[right];
        right++;
        if (need.count(c)) {
            window[c]++;
            if (window[c] == need[c])
                valid++;
        }

        while (right - left >= p.size()) {
            if (valid == need.size()) res.push_back(left);
            char d = s[left];
            left++;
            if (need.count(d)) {
                if (window[d] == need[d]) valid--;
                window[d]--;
            }
        }
    }
    return res;
}

位运算

二进制中1的个数

1
2
3
4
5
6
7
8
int hammingWeight(uint32_t n) {
    int res = 0;
    while (n > 0) {
        if (n & 1 == 1) res++;
        n >>= 1;
    }
    return res;
}

不用加减乘除左加法

1
2
3
4
5
6
7
8
9
int add(int a, int b) {
    while(b != 0)
    {
        int c = (unsigned int)(a & b) << 1;
        a ^= b;
        b = c;
    }
    return a;
}

剪绳子

1
2
3
4
5
6
7
8
9
10
11
12
int cuttingRope(int n) {
    if (n <= 3) return n-1;
    int b = n % 3, p = 1000000007;
    long rem = 1, x = 3;
    for (int a = n / 3 - 1; a > 0; a /= 2) {
        if (a % 2 == 1) rem = (rem * x) % p;
        x = (x * x) % p;
    }
    if (b == 0) return (int)(rem*3%p);
    if (b == 1) return (int)(rem*4%p);
    return (int)(rem*6%p);
}

1~n整数中1出现的次数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
int countDigitOne(int n) {
    long digit = 1;
    int high = n / 10, cur = n % 10, low = 0, res = 0;
    while (high != 0 || cur != 0) {
        if (cur == 0) res += high * digit;
        else if (cur == 1) res += high * digit + low + 1;
        else res += (high + 1) * digit;
        low += cur * digit;
        cur = high % 10;
        high /= 10;
        digit *= 10;
    }
    return res;
}

数字序列中的某一位数字

1
2
3
4
5
6
7
8
9
10
11
12
13
14
int findNthDigit(int n) {
    if (n < 10) return n;
    int digit = 1;
    long start = 1;
    long count = 9;
    while (n > count) {
        n -= count;
        start *= 10;
        digit += 1;
        count = digit * start * 9;
    }
    long num = start + (n - 1) / digit;
    return to_string(num)[(n - 1) % digit] - '0';
}

构建乘积数组

1
2
3
4
5
6
7
8
9
10
11
12
13
14
vector<int> constructArr(vector<int>& a) {
    int len = a.size();
    if (len == 0) return {};
    vector<int> res(len, 1);
    int temp = 1;
    for (int i = 1; i < len; ++i) {
        res[i] = res[i-1] * a[i-1];
    }
    for (int i = len - 2; i >=0; i--) {
        temp *= a[i+1];
        res[i] *= temp;
    }
    return res;
}

模拟

顺时针打印矩阵

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
vector<int> spiralOrder(vector<vector<int>>& matrix) {
    if (matrix.empty()) return {};
    vector<int> res;
    int left = 0, right = matrix[0].size()-1, top = 0, down = matrix.size()-1;
    while (true) {
        for (int i = left; i <= right; ++i) {
            res.push_back(matrix[top][i]);
        }
        if (++top > down) break;
        for (int i = top; i <= down; ++i) {
            res.push_back(matrix[i][right]);
        }
        if (--right < left) break;
        for (int i = right; i >= left; --i) {
            res.push_back(matrix[down][i]);
        }
        if (--down < top) break;
        for (int i = down; i >= top; --i) {
            res.push_back(matrix[i][left]);
        }
        if (++left > right) break;
    }
    return res;
}

栈的压入、弹出序列

1
2
3
4
5
6
7
8
9
10
11
12
bool validateStackSequences(vector<int>& pushed, vector<int>& popped) {
    stack<int> stk;
    int i = 0;
    for (int num : pushed) {
        stk.push(num);
        while (!stk.empty() && stk.top() == popped[i]) {
            stk.pop();
            i++;
        }
    }
    return stk.empty();
}